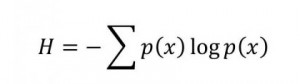Research can flow into interesting little eddies that cohere into larger circulations that become transformative phase shifts. That happened to me this morning between a morning drive in the Northern California hills and departing for lunch at one of our favorite restaurants in Danville.

The topic I’ve been working on since my retirement is whether there are preferential representations for optimal automated inference methods. We have this grab-bag of machine learning techniques that use differing data structures but that all implement some variation on fitting functions to data exemplars; at the most general they all look like some kind of gradient descent on an error surface. Getting the right mix of parameters, nodes, etc. falls to some kind of statistical regularization or bottlenecking for the algorithms. Or maybe you perform a grid search in the hyperparameter space, narrowing down the right mix. Or you can throw up your hands and try to evolve your way to a solution, suspecting that there may be local optima that are distracting the algorithms from global success.

Yet, algorithmic information theory (AIT) gives us, via Solomonoff, a framework for balancing parameterization of an inference algorithm against the error rate on the training set. But, first, it’s all uncomputable and, second, the AIT framework just uses strings of binary as the coded Turing machines, so I would have to flip 2^N bits and test each representation to get anywhere with the theory. Yet, I and many others have had incremental success at using variations on this framework, whether via Minimum Description Length (MDL) principles, it’s first cousin Minimum Message Length (MML), and other statistical regularization approaches that are somewhat proxies for these techniques.… Read the rest